vDSPを使う（高速フーリエ変換編その4）

簡単な高速フーリエ変換ができるようになりましたが、なにも考えずに信号をフーリエ変換すると周波数特性がきれいにでない場合があります。これは信号に含まれる成分の波長がフーリエ変換する長さに会わなかった場合に発生するのですが、「窓」と呼ばれるものを使うとこの問題を低減できます。「窓」を作る機能もvDSPには用意されているので使ってみます。

「窓」を作る前に、どういう問題なの？

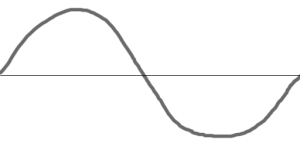
離散フーリエ変換では、特性上信号（配列）の長さにぴったりおさまる波形はキレイに解析できるのですが、

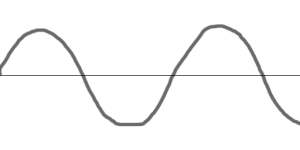
波長が信号（配列）の長さにおさまらない波形はキレイに解析できません。
前の記事で最初に作った波形は30回振動する周期(つまり、波長が配列の長さの1/30になっている)ので、波形がぴったり配列におさまりキレイな周波数特性がでるのですが、これの周期を中途半端な少数などにしてしまうと、キレイな周波数特性はでなくなってしまいます。現実世界に存在する音声信号は基本的に後者（配列の長さに波長がぴったりおさまることはない）なので、これでは問題です。

これは、こうやって信号を並べた時に両端に不連続な個所が発生してしまうためだとイメージしてください。

どうするの？

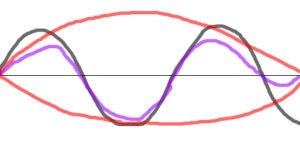
じゃあ波形の両端をつまんで0にしちゃって、無理矢理つながるようにしようぜ
という発想です。

窓関数

この、「両端をつまんで0にする」ために元の信号に対してかけ算をするのですが、その時に使われる関数のことを窓関数と言います。
窓関数にはいくつか種類がありますが、vDSPの中にも用意されています。今回はその中でもシンプルなハニング窓というのを使います。

窓関数の使い方

窓を作る

窓関数の使い方はちょっと特殊です。最初にvDSP_hann_window関数を使って「窓」を作ります。vDSP_hann_window関数では、

作った「窓」を入れるための配列の場所
「窓」の長さ
半分までしか作らないか、全体をつくるか

を引数で渡します。窓の長さはフーリエ変換させる信号の長さと同じ長さ、最後の引数では0を指定して窓を最後まで作ってもらうようにします。

// ハニング窓を作ります
float windowWave[512];
vDSP_hann_window(windowWave, 512, 0);

窓がどうなっているか気になる人は、ログに出力してみてください。

for (int i=0; i < 512; i++) {
	NSLog(@"[%d] %f", windowWave[i]);
}

信号に窓をかける

元の信号に「窓」を掛けます。勿論、信号のかけ算にもvDSPの加減乗除の関数を使いましょう。

// 窓を入力信号にかけます
float windowedInputWave[512];
vDSP_vmul(inputWave, 1, windowWave, 1, windowedInputWave, 1, 512);

信号の両端の音量が0になってつなぎ目がきれいになった信号windowedInputWaveができました。

フーリエ変換する

あとは、この両端が0になった信号を前回と同じく複素数に変換してから、フーリエ変換するだけです。

// 複素数に変換します
DSPSplitComplex splitComplex;
splitComplex.realp = calloc(512, sizeof(float));
splitComplex.imagp = calloc(512, sizeof(float));
for (int i=0; i<512; i++) {
	splitComplex.realp[i] = windowedInputWave[i];
}
// フーリエ変換します
FFTSetup fftSetup = vDSP_create_fftsetup(9, FFT_RADIX2);
vDSP_fft_zrip(fftSetup, &splitComplex, 1, 9, FFT_FORWARD);
vDSP_destroy_fftsetup(fftSetup);

窓を使わなかった場合に比べて、周波数特性が正しくとれているはずなので周波数特性を出力して、確認してみてください。

Pocket